DictionaryInversionally |
| Buy sheetmusic at SheetMusicPlus |
In music theory, the word inversion has several meanings. There are inverted chords, inverted melodies, inverted intervals, and (in counterpoint) inverted voices. The concept of inversion also plays a role in musical set theory.
Inverted intervals
Interval complementation: P4 + P5 = P8
An interval is inverted by raising or lowering either of the notes one octave, so that both retain their names (pitch class) and the one which was higher is now lower and vice versa, changing the perspective or relation between the pitch classes. For example, the inversion of an interval consisting of a C with an E above it is an E with a C above it - to work this out, the C may be moved up, the E may be lowered, or both may be moved. (The only exception to the "swap" rule is that a diminished unison is the inversion of an augmented octave but the higher note is still higher.) Under inversion, perfect intervals remain perfect, major intervals become minor and the reverse, augmented intervals become diminished and the reverse. (Double diminished intervals become double augmented intervals, and the reverse.) Traditional interval names add together to make nine: seconds become sevenths and the reverse, thirds become sixes and the reverse, and fourths become fifths and the reverse. Thus a perfect fourth becomes a perfect fifth, an augmented fourth becomes a diminished fifth, and a simple interval (that is, one that is narrower than an octave) and its inversion, when added together, will equal an octave. See also complement (music).
Inverted chords
Figure 1: the closing phrase of the hymn-setting Rustington by the English composer Hubert Parry (1848–1918),[1] showing all three positions of the C major chord.[2] See figured bass below for a description of the numerical symbols.
A chord's inversion describes the relationship of its bass to the other tones in the chord. For instance, a C major triad contains the tones C, E and G; its inversion is determined by which of these tones is used as the bottom note in the chord. The term inversion is often used to categorically refer to the different possibilities, although it may also be restricted to only those chords where the bass note is not also the root of the chord (see root position below). In texts that make this restriction, the term position may be used instead to refer to all of the possibilities as a category. Root positionMain article: Root (chord)
A root-position chord The following chord is also a C major triad in root position, since the root is still in the bass. The rearrangement of the notes above the bass into different octaves (here, the note E) and the doubling of notes (here, G), is known as voicing. InversionsIn an inverted chord, the root is not in the bass (i.e., is not the lowest note). The inversions are numbered in the order their bass tones would appear in a closed root position chord (from bottom to top). In the first inversion of a C major triad In the second inversion Third inversions exist only for chords of four or more tones, such as 7th chords. In a third-inversion chord Notating root position and inversionsFigured bassMain article: Figured bass
Figured bass is notation convention used to specify chord inversion, in which Arabic numerals (figures) are written (placed vertically, in descending numerical order) below the bass note of each chord in a harmonic progression, expressing the intervals resulting from the voices above it (usually assuming octave equivalence). For example, in root-position triad C-E-G, the intervals above bass note C are a 3rd and a 5th, giving the figures Certain arbitrary conventions of abbreviation (and sometimes non-abbreviation) exist in the use of figured bass. In chords whose bass notes appear without symbols, Figured bass numerals express distinct intervals in a chord only as they relate to the bass voice. They make no reference to the key of the progression (unlike roman-numeral harmonic analysis); They do not express intervals between pairs of upper voices themselves (for example, in a C-E-G triad, figured bass is unconcerned with the interval relationship E-G); They do not express tones in upper voices which double, or are unison with, the bass note. However, the figures are often used on their own (without the bass) in music theory simply to specify a chord's inversion. This is the basis for the terms given above such as " Popular-music notationMain article: Slash chord
A notation for chord inversion often used in popular music is to write the name of a chord followed by a forward slash and then the name of the bass note. For example, the C chord above, in first inversion (i.e., with E in the bass) may be notated as C/E. This notation works even when a note not present in a triad is the bass; for example, F/G is a way of notating a particular approach to voicing a G11th chord (G–F–A–C). (This is quite different from analytical notations of function; e.g., the use of IV/V or S/D to represent the subdominant of the dominant). Lower-case lettersLower-case letters may be placed after a chord symbol to indicate root position or inversion.[3] Hence, in the key of C major, the C major chord below in first inversion may be notated as Ib, indicating chord I, first inversion. (Less commonly, the root of the chord is named, followed by a lower-case letter: Cb). If no letter is added, the chord is assumed to be in root inversion, as though A had been inserted. Arabic numeralsA less common notation is to place the number 1, 2 or 3 etc. after a chord to indicate that it is in first, second, or third inversion respectively. The C chord above in root position is notated as C, and in first inversion as C1.[citation needed] (This notation is quite different from the Arabic numerals placed after note names to indicate the octave of a tone, typically used in acoustical contexts; for example, C4 is often used to mean the single tone middle C, and C3 the tone an octave below it.)
Cadential six-four chord (or Appoggiatura six-four chord)The cadential
CounterpointContrapuntal inversion requires that two melodies, having accompanied each other once, do it again with the melody that had been in the high voice now in the low, and vice versa. Also called "double counterpoint" (if two voices are involved) or "triple counterpoint" (if three), themes that can be developed in this way are said to involve themselves in "invertible counterpoint." The action of changing the voices is called "textural inversion". Invertible counterpoint can occur at various intervals, usually the octave (8va), less often at the 10th or 12th. To calculate the interval of inversion, add the intervals by which each voice has moved and subtract one. For example: If motive A in the high voice moves down a 6th, and motive B in the low voice moves up a 5th, in such a way as to result in A and B having exchanged registers, then the two are in double counterpoint at the 10th ((6+5)–1 = 10). Invertible counterpoint achieves its highest expression in the four canons of JS Bach's Art of Fugue, with the first canon at the octave, the second canon at the 10th, the third canon at the 12th, and the fourth canon in augmentation and contrary motion. Other exemplars can be found in the fugues in G minor and B-flat major [external Shockwave movies] from Book II of Bach's Well-Tempered Clavier, both of which contain invertible counterpoint at the octave, 10th, and 12th. Inverted melodies
Figure 4: Inversion of the melody in Rachmaninoff's Rhapsody on a Theme by Paganini
When applied to melodies, the inversion of a given melody is the melody turned upside-down. For instance, if the original melody has a rising major third (see interval), the inverted melody has a falling major third (or perhaps more likely, in tonal music, a falling minor third, or even some other falling interval). Similarly, in twelve-tone technique, the inversion of the tone row is the so-called prime series turned upside-down. See m. 24 of Bach's C#m fugue [external Shockwave movie], Well-Tempered Clavier 2, for an example of the subject in its melodic inversion. Inversional equivalencyInversional equivalency or inversional symmetry is the concept that intervals, chords, and other sets of pitches are the same when inverted. It is similar to enharmonic equivalency and octave equivalency and even transpositional equivalency. Inversional equivalency is used little in tonal theory, though it is assumed a set which may be inverted onto another are remotely in common. However, taking them to be identical or near-identical is only assumed in musical set theory. All sets of pitches with inversional symmetry have a center or axis of inversion. For example, the set C–E–F–F♯–G–B has one center at the dyad F and F♯ and another at the tritone, B/C, if listed F♯–G–B–C–E–F. For C–E♭–E–F♯–G–B♭ the center is F and B if listed F♯–G–B♭–C–E♭–E.[9]. Musical set theoryMain article: set (music)
In musical set theory inversion may be usefully thought of as the compound operation transpositional inversion, which is the same sense of inversion as in the Inverted melodies section above, with transposition carried out after inversion. Pitch inversion by an ordered pitch interval may be defined as: which equals First invert the pitch or pitches, x = −x, then transpose, −x + n. Pitch class inversion by a pitch class interval may be defined as: Inversion about a pitch axis is a compound operation much like set theory's transpositional inversion, however in pitch axis inversion the transposition may be chromatic or diatonic transposition. Pitch axisIn jazz theory, a pitch axis is the center about which a melody is inverted[10]. The "pitch axis" works in the context of the compound operation transpositional inversion, where transposition is carried out after inversion, however unlike musical set theory the transposition may be chromatic or diatonic transposition. Thus if D-A-G (P5 up, M2 down) is inverted to D-G-A (P5 down, M2 up) the "pitch axis" was or will be D. However, if it is inverted to C-F-G the pitch axis is G while if the pitch axis is A, the melody will invert to E-A-B. Note that the notation of octave position may determine how many lines and spaces appears to share the axis. The pitch axis of D-A-G and its inversion A-D-E will either appear to be between C/B♮ or the single pitch F. HistoryIn the theories of Rameau (1722), chords in different positions were considered functionally equivalent. However, theories of counterpoint before Rameau spoke of different intervals in different ways, such as the regola delle terze e seste ("rule of sixths and thirds") which required the resolution of imperfect consonances to perfect ones, and would not propose a similarity between See alsoReferences
| |||||||||||||||||||
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Inversionally". Allthough most Wikipedia articles provide accurate information accuracy can not be guaranteed. | |||||||||||||||||||
Help us with donations or by making music available!
©2023 Classic Cat - the classical music directory

Beethoven, L. van
Piano Sonata No. 29 "Hammerklavier"
Paavali Jumppanen
Beethoven, L. van
Symphony No. 3 "Eroica"
Deutsches Symphonie Orchester Berlin
Vivaldi, A.
Spring
Stuttgart Chamber Orchestra
Paganini, N.
24 Caprices
Salvatore Accardo
Tchaikovsky, P.I.
Piano Concerto no. 1
Dimitris Sgouros
Vivaldi, A.
Spring
Stuttgart Chamber Orchestra


 chord.
chord.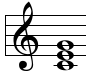

 chord.
chord.
 chord. This inversion can be either
chord. This inversion can be either 


 , i.e. presence of the 3rd is understood. Second-inversion triads (
, i.e. presence of the 3rd is understood. Second-inversion triads (  . First inversion seventh-chords 6-5-3, are abbreviated as
. First inversion seventh-chords 6-5-3, are abbreviated as  . Second inversion seventh-chords 6-4-3, are abbreviated as
. Second inversion seventh-chords 6-4-3, are abbreviated as  . Third inversion seventh-chords 6-4-2 are abbreviated as
. Third inversion seventh-chords 6-4-2 are abbreviated as  .
. refers to a tonic triad in first inversion.
refers to a tonic triad in first inversion.
 . Most older harmony textbooks use this label, and it can be traced back to the early 19th century
. Most older harmony textbooks use this label, and it can be traced back to the early 19th century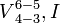 , in which the
, in which the  chord, but a dissonance that resolves to
chord, but a dissonance that resolves to  (that is,
(that is,  ). This function is very similar to the resolution of a 4–3
). This function is very similar to the resolution of a 4–3 


