DictionaryPitch class |
| Buy sheetmusic at SheetMusicPlus |
|
In music, a pitch class is a set of all pitches that are a whole number of octaves apart, e.g., the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave position."[1] Thus, using scientific pitch notation, the pitch class "C" is the infinite set
Pitch class is important because human pitch-perception is periodic: pitches belonging to the same pitch class are perceived as having a similar "quality" or "color", a phenomenon called octave equivalence. Psychologists refer to the quality of a pitch as its "chroma". A "chroma" is an attribute of pitches, just like hue is an attribute of color. A "pitch class" is a set of all pitches sharing the same chroma, just like "the set of all white things" is the collection of all white objects.[citation needed] Note that in standard Western equal temperament, distinct spellings can refer to the same sounding object: B♯3, C4, and D
Integer notationTo avoid the problem of enharmonic spellings, theorists typically represent pitch classes using numbers. One can map a pitch's fundamental frequency f (measured in hertz) to a real number p using the equation
This creates a linear pitch space in which octaves have size 12, semitones (the distance between adjacent keys on the piano keyboard) have size 1, and middle C is assigned the number 60. Indeed, the mapping from pitch to real numbers defined in this manner forms the basis of the MIDI Tuning Standard, which uses the real numbers from 0 to 127 to represent the pitches C-1 to G9. To represent pitch classes, we need to identify or "glue together" all pitches belonging to the same pitch class—i.e. all numbers p and p + 12. The result is a circular quotient space that musicians call pitch class space and mathematicians call R/12Z. Points in this space can be labelled using real numbers in the range 0 ≤ x < 12. These numbers provide numerical alternatives to the letter names of elementary music theory:
and so on. In this system, pitch classes represented by integers are classes of twelve-tone equal temperament (assuming standard concert A). To avoid confusing 10 with 1 and 0, some theorists assign pitch classes 10 and 11 the letters "t" (after "ten") and "e" (after "eleven"), respectively (or A and B, as in the writings of Allen Forte and Robert Morris). In music, integer notation is the translation of pitch classes and/or interval classes into whole numbers.[2] Thus C=0, C#=1 ... A#=10, B=11, with "10" and "11" substituted by "t" and "e" in some sources[2] This allows the most economical presentation of information regarding post-tonal materials.[2] In the integer model of pitch, all pitch classes and intervals between pitch classes are designated using the numbers 0 through 11. It is not used to notate music for performance, but is a common analytical and compositional tool when working with chromatic music, including twelve tone, serial, or otherwise atonal music. Pitch classes can be notated in this way by assigning the number 0 to some note—C natural by convention[citation needed]—and assigning consecutive integers to consecutive semitones; so if 0 is C natural, 1 is C sharp, 2 is D natural and so on up to 11, which is B natural. The C above this is not 12, but 0 again (12-12=0). Thus arithmetic modulo 12 is used to represent octave equivalence. One advantage of this system is that it ignores the "spelling" of notes (B sharp, C natural and D double-flat are all 0) according to their diatonic functionality. There are a few disadvantages with integer notation. First, theorists have traditionally used the same integers to indicate elements of different tuning systems. Thus, the numbers 0, 1, 2, ... 5, are used to notate pitch classes in 6-tone equal temperament. This means that the meaning of a given integer changes with the underlying tuning system: "1" can refer to C♯ in 12-tone equal temperament, but D in 6-tone equal temperament. Also, the same numbers are used to represent both pitches and intervals. For example, the number 4 serves both as a label for the pitch class E (if C=0) and as a label for the distance between the pitch classes D and F♯. (In much the same way, the term "10 degrees" can function as a label both for a temperature, and for the distance between two temperatures.) Only one of these labelings is sensitive to the (arbitrary) choice of pitch class 0. For example, if one makes a different choice about which pitch class is labeled 0, then the pitch class E will no longer be labelled "4." However, the distance between D and F♯ will still be assigned the number 4. The late music theorist David Lewin was particularly sensitive to the confusions that this can cause[example needed], and both this and the above may be viewed as disadvantages. Additionally, integer notation does not seem to allow for the notation of microtones, or notes not belonging to the underlying equal division of the octave. For these reasons, some theorists have recently advocated using rational numbers to represent pitches and pitch classes, in a way that is not dependent on any underlying division of the octave. Other ways to label pitch classes
The system described above is flexible enough to describe any pitch class in any tuning system: for example, one can use the numbers {0, 2.4, 4.8, 7.2, 9.6} to refer to the five-tone scale that divides the octave evenly. However, in some contexts, it is convenient to use alternative labeling systems. For example, in just intonation, we may express pitches in terms of positive rational numbers p/q, expressed by reference to a 1 (often written "1/1"), which represents a fixed pitch. If a and b are two positive rational numbers, they belong to the same pitch class if and only if for some integer n. Therefore, we can represent pitch classes in this system using ratios p/q where neither p nor q is divisible by 2, that is, as ratios of odd integers. Alternatively, we can represent just intonation pitch classes by reducing to the octave, It is also very common to label pitch classes with reference to some scale. For example, one can label the pitch classes of n-tone equal temperament using the integers 0 to n-1. In much the same way, one could label the pitch classes of the C major scale, C-D-E-F-G-A-B using the numbers from 0 to 6. This system has two advantages over the continuous labeling system described above. First, it eliminates any suggestion that there is something natural about a 12-fold division of the octave. Second, it avoids pitch-class universes with unwieldy decimal expansions when considered relative to 12; for example, in the continuous system, the pitch-classes of 19-tet are labeled 0.63158... , 1.26316... , etc. Labeling these pitch classes {0, 1, 2, 3 ... , 18} simplifies the arithmetic used in pitch-class set manipulations. The disadvantage of the scale-based system is that it assigns an infinite number of different names to chords that sound identical. For example, in twelve-tone equal-temperament the C major triad is notated {0, 4, 7}. In twenty-four-tone equal-temperament, this same triad is labeled {0, 8, 14}. Moreover, the scale-based system appears to suggest that different tuning systems use steps of the same size ("1") but have octaves of differing size ("12" in 12-tone equal-temperament, "19" in 19-tone equal temperament, and so on), whereas in fact the opposite is true: different tuning systems divide the same octave into different-sized steps. In general, it is often more useful to use the traditional integer system when one is working within a single temperament; when one is comparing chords in different temperaments, the continuous system can be more useful. See alsoSources
Further reading
| ||||||||||||||||||||||||||||||||||||||||||||||||||
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Pitch class". Allthough most Wikipedia articles provide accurate information accuracy can not be guaranteed. | ||||||||||||||||||||||||||||||||||||||||||||||||||
Help us with donations or by making music available!
©2023 Classic Cat - the classical music directory

Tchaikovsky, P.I.
The Nutcracker - suite
Goose Creek Bands
Beethoven, L. van
Piano Concerto No. 5 "Emperor"
Dimitris Sgouros
Mendelssohn-Bartholdy, F.
Violin Concerto in E minor
New York Philharmonic Orchestra
Mozart, W.A.
Bassoon Concerto
Soni Ventorum Wind Quintet
Strauss, R.
An Alpine Symphony
Deutsches Symphonie Orchester Berlin
Verdi, G.
Nabucco
Choeur Des Marias




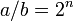
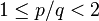 .
.