DictionaryMathematics of musical scales |
| Buy sheetmusic at SheetMusicPlus |

A spectrogram of a violin waveform, with linear frequency on the vertical axis and time on the horizontal axis. The bright lines show how the spectral components change over time. The intensity coloring is logarithmic (black is −120 dBFS).
Music theorists often use mathematics to understand music. Indeed, mathematics is "the basis of sound" and sound itself "in its musical aspects... exhibits a remarkable array of number properties", simply because nature itself "is amazingly mathematical".[1] Though ancient Chinese, Egyptians and Mesopotamians are known to have studied the mathematical principles of sound,[2] the Pythagoreans of ancient Greece are the first researchers known to have investigated the expression of musical scales in terms of numerical ratios,[3] particularly the ratios of small integers. Their central doctrine was that "all nature consists of harmony arising out of number".[4] From the time of Plato harmony was considered a fundamental branch of physics, now known as musical acoustics. Early Indian and Chinese theorists show similar approaches: all sought to show that the mathematical laws of harmonics and rhythms were fundamental not only to our understanding of the world but to human well-being.[5] Confucius, like Pythagoras, regarded the small numbers 1,2,3,4 as the source of all perfection.[6] The attempt to structure and communicate new ways of composing and hearing music has led to musical applications of set theory, abstract algebra and number theory. Some composers have incorporated the Golden ratio and Fibonacci numbers into their work.[7][8]
Time, rhythm and metreMain article: Meter (music)
Without the boundaries of rhythmic structure - a fundamental equal and regular arrangement of pulse repetivity, accent, phrase and duration - music would be impossible.[9] In Old English the word "rhyme", derived from "rhythm", became associated and confused with rim - "number"[10] - and modern musical use of terms like metre and measure also reflect the historical importance of music, along with astronomy, in the development of counting, arithmetic and the exact measurement of time and periodicity that is fundamental to physics. Musical formMain article: Musical form
Musical form is the plan by which a short piece of music is extended. The term "plan" is also used in architecture, to which musical form is often compared. Like the architect, the composer must take into account the function for which the work is intended and the means available, practising economy and making use of repetition and order.[11] The common types of form known as binary and ternary ("twofold" and "threefold") once again demonstrate the importance of small integral values to the intelligibility and appeal of music. Frequency and harmony
Chladni figures produced by sound vibrations in fine powder on a square plate. (Ernst Chladni, Acoustics, 1802)
A musical scale is a discrete set of pitches used in making or describing music. The most important scale in the Western tradition is the diatonic scale but many others have been used and proposed in various historical eras and parts of the world. Each pitch corresponds to a particular frequency, expressed in hertz (Hz), sometimes referred to as cycles per second (c.p.s.). A scale has an interval of repetition, normally the octave. The octave of any pitch refers to a frequency exactly twice that of the given pitch. Succeeding superoctaves are pitches found at frequencies four, eight, sixteen times, and so on, of the fundamental frequency. Pitches at frequencies of half, a quarter, an eighth and so on of the fundamental are called suboctaves. There is no case in musical harmony where, if a given pitch be considered accordant, that its octaves are considered otherwise. Therefore any note and its octaves will generally be found similarly named in musical systems (e.g. all will be called doh or A or Sa, as the case may be). When expressed as a frequency bandwidth an octave A-A spans from 110 Hz to 220 Hz (span=110 Hz). The next octave will span from 220 Hz to 440 Hz (span=220 Hz). The third octave spans from 440 Hz to 880 Hz (span=440 Hz) and so on. Each successive octave spans twice the frequency range of the previous octave. Human ears interpret all octaves as spanning a range of pitches the same size, even though a sub-bass octave may span 40 Hz and a super-treble octave can span 4000 Hz. Because we are often interested in the relations or ratios between the pitches (known as intervals) rather than the precise pitches themselves in describing a scale, it is usual to refer all the scale pitches in terms of their ratio from a particular pitch, which is given the value of one (often written 1/1), generally a note which functions as the tonic of the scale. For interval size comparison cents are often used.
Tuning systemsMain articles: Musical tuning and Musical temperament
5-limit tuning, the most common form of Just intonation, is a system of tuning using tones that are regular number harmonics of a single fundamental frequency. This was one of the scales Johannes Kepler presented in his Harmonice Mundi (1619) in connection with planetary motion. The same scale was given in transposed form by Alexander Malcolm in 1721 and by theorist Jose Wuerschmidt in the 20th century. A form of it is used in the music of northern India. American composer Terry Riley also made use of the inverted form of it in his "Harp of New Albion". Just intonation gives superior results when there is little or no chord progression: voices and other instruments gravitate to just intonation whenever possible. However, as it gives two different whole tone intervals (9:8 and 10:9) a keyboard instrument so tuned cannot change key.[12] To calculate the frequency of a note in a scale given in terms of ratios, the frequency ratio is multiplied by the tonic frequency. For instance, with a tonic of A4 (A natural above middle C), the frequency is 440 Hz, and a justly tuned fifth above it (E5) is simply 440*(3:2) = 660 Hz.
Pythagorean tuning is tuning based only on the perfect consonances, the (perfect) octave, perfect fifth, and perfect fourth. Thus the major third is considered not a third but a ditone, literally "two tones", and is 81:64 = (9:8)², rather than the independent and harmonic just 5:4, directly below. A whole tone is a secondary interval, being derived from two perfect fifths, (3:2)^2 = 9:8. The just major third, 5:4 and minor third, 6:5, are a syntonic comma, 81:80, apart from their Pythagorean equivalents 81:64 and 32:27 respectively. According to Carl Dahlhaus (1990, p. 187), "the dependent third conforms to the Pythagorean, the independent third to the harmonic tuning of intervals." Western common practice music usually cannot be played in just intonation but requires a systematically tempered scale. The tempering can involve either the irregularities of well temperament or be constructed as a regular temperament, either some form of equal temperament or some other regular meantone, but in all cases will involve the fundamental features of meantone temperament. For example, the root of chord ii, if tuned to a fifth above the dominant, would be a major whole tone (9:8) above the tonic. If tuned a just minor third (6:5) below a just subdominant degree of 4:3, however, the interval from the tonic would equal a minor whole tone (10:9) Meantone temperament reduces the difference between 9:8 and 10:9. Their ratio, (9:8)/(10:9) = 81:80, is treated as a unison. The interval 81:80, called the syntonic comma or comma of Didymus, is the key comma of meantone temperament. In equal temperament, the octave is divided into twelve equal parts, each semitone (half step) is an interval of the twelfth root of two so that twelve of these equal half steps add up to exactly an octave. With fretted instruments it is very useful to use an equal tempering so that the frets align evenly across the strings. In the European music tradition, equal tempering was used for lute and guitar music far earlier than for other instruments. Equally-tempered scales have been used and instruments built using various other numbers of equal intervals. The 19 equal temperament, first proposed and used by Guillaume Costeley in the sixteenth century, uses 19 equally spaced tones, offering better major thirds and far better minor thirds than normal 12-semitone equal temperament at the cost of a flatter fifth. The overall effect is one of greater consonance. 24 equal temperament, with 24 equally spaced tones, is widespread in Arabic music. The following graph reveals how accurately various equal tempered scales approximate three important harmonic identities: the major third (5th harmonic), the perfect fifth (3rd harmonic), and the "harmonic seventh" (7th harmonic). [Note: the numbers above the bars designate the equal tempered scale (I.e., "12" designates the 12-tone equal tempered scale, etc.)]
Below are Ogg Vorbis files demonstrating the difference between just intonation and equal temperament. You may need to play the samples several times before you can pick the difference.
Connections to set theoryMain article: Set theory (music)
Musical set theory uses some of the concepts from mathematical set theory to organize musical objects and describe their relationships. To analyze the structure of a piece of (typically atonal) music using musical set theory, one usually starts with a set of tones, which could form motives or chords. By applying simple operations such as transposition and inversion, one can discover deep structures in the music. Operations such as transposition and inversion are called isometries because they preserve the intervals between tones in a set. Connections to abstract algebraMain article: Abstract algebra
Expanding on the methods of musical set theory, many theorists have used abstract algebra to analyze music. For example, the notes in an equal temperament octave form an abelian group with 12 elements. It is possible to describe just intonation in terms of a free abelian group.[13] Transformational theory is a branch of music theory developed by David Lewin. The theory allows for great generality because it emphasizes transformations between musical objects, rather than the musical objects themselves. Theorists have also proposed musical applications of more sophisticated algebraic concepts. Mathematician Guerino Mazzola has applied topos theory to music[citation needed], though the result has been controversial[citation needed]. The chromatic scale has a free and transitive action of Connections to number theoryMain article: Number theory
Modern interpretation of just intonation is fully based on fundamental theorem of arithmetic. The golden ratio and Fibonacci numbersIt is believed that some composers wrote their music using the golden ratio and the Fibonacci numbers to assist them.[14] However, regarding the listener, the degree to which the application of the golden ratio in music is salient, whether consciously or unconsciously, as well as the overall musical effect of its implementation, if any, is unknown. James Tenney reconceived his piece "For Ann (Rising)", which consists of up to twelve computer-generated tones that glissando upwards (see Shepard tone), as having each tone start so each is the golden ratio (in between an equal tempered minor and major sixth) below the previous tone, so that the combination tones produced by all consecutive tones are a lower or higher pitch already, or soon to be, produced. Ernő Lendvai analyzes Béla Bartók's works as being based on two opposing systems: those of the golden ratio and the acoustic scale. In Bartok's Music for Strings, Percussion, and Celesta, the xylophone progression at the beginning of the 3rd movement occurs at the intervals 1:2:3:5:8:5:3:2:1. French composer Erik Satie used the golden ratio in several of his pieces, including Sonneries de la Rose Croix. His use of the ratio gave his music an otherworldly symmetry. The golden ratio is also apparent in the organization of the sections in the music of Debussy's Image, "Reflections in Water", in which the sequence of keys is marked out by the intervals 34, 21, 13, and 8 (a descending Fibonacci sequence), and the main climax sits at the φ position. Tool use a large number of numerical references to the Fibonacci sequence and the Golden ratio in the song "Lateralus" from the album of the same name. The delivery of the words in the song are timed so that the syllables follow the Fibonacci sequence as well (1,1,2,3,5,8,5,3,2,1,1). This Binary Universe, an experimental album by Brian Transeau (popularly known as the electronic artist BT), includes a track titled 1.618 in homage to the golden ratio. The track features musical versions of the ratio and the accompanying video displays various animated versions of the golden mean. See also
References
External links
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Mathematics of musical scales". Allthough most Wikipedia articles provide accurate information accuracy can not be guaranteed. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Help us with donations or by making music available!
©2023 Classic Cat - the classical music directory

Ornstein, L.
4 Impromptus
Christopher Oldfather
Wagner, R.
Die Meistersinger von Nürnberg
Bayerischen Staatsoper
Mozart, W.A.
Concerto for Flute & Harp
Mary Angelina Mei
Tchaikovsky, P.I.
Piano Concerto no. 1
Dimitris Sgouros
Saint-Saëns, C.
Introduction and Rondo Capriccioso
Steven Cheng
Tchaikovsky, P.I.
Piano Concerto no. 1
Dimitris Sgouros



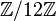 , with the action being defined via
, with the action being defined via